In this lesson, you'll learn about trees and graphs, which are important data structures in computer science. You'll represent them using simple Python structures like dictionaries and lists, implement depth-first search (DFS) and breadth-first search (BFS) traversals, and apply them to a maze path-finding project in VS Code.

By the end of this lesson, you will be able to:

• Explain the concepts of trees and graphs.
• Represent trees and graphs in Python.
• Implement DFS and BFS traversals.
• Apply traversals to solve a path-finding problem in a maze.

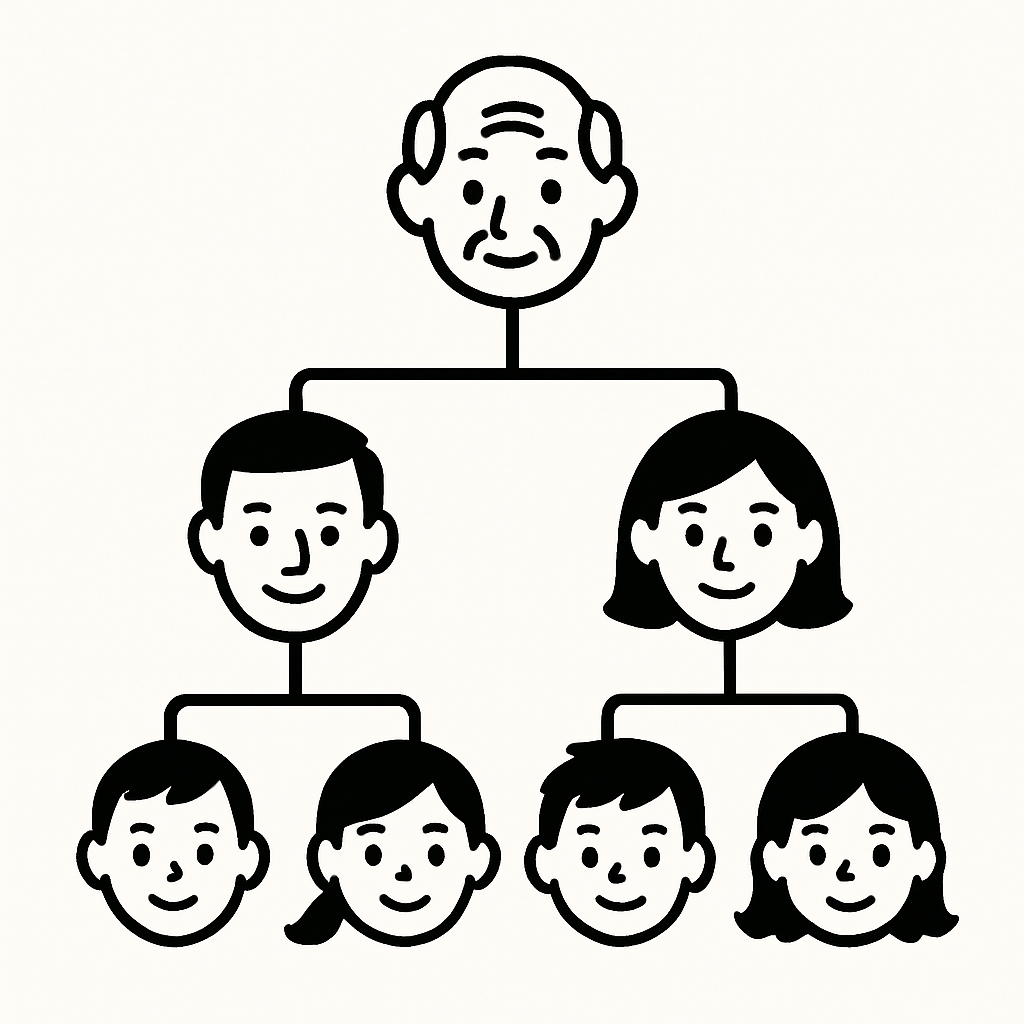A tree is a hierarchical data structure consisting of nodes connected by edges, with no cycles. It has a root node, and each node can have child nodes. Trees are used in file systems, organisation charts, and decision-making algorithms.

Key terms:

• Root: The top node with no parent.
• Leaf: A node with no children.
• Edge: Connection between nodes.
• Height: The longest path from root to leaf.

For example, a family tree starts with a root (grandparent) and branches to children and grandchildren. This branching structure allows trees to represent relationships where one item can lead to multiple others, like folders containing subfolders in a computer file system.

We can represent a tree using a dictionary where keys are nodes and values are lists of children. This is a simple way to model the hierarchical structure of a tree in Python, where each key represents a parent node, and the list shows its direct children. For example, if 'A' has children 'B' and 'C', it means 'A' is the parent, and 'B' and 'C' branch out from it.

Imagine the tree looking like this: 'A' at the top, connected down to 'B' and 'C'. From 'B', it branches to 'D' and 'E', and from 'C' to 'F'. 'D', 'E', and 'F' are leaves since they have no children.

Create a file named 'tree.py' in your 'TreesGraphs' folder.

Add the following code to represent a simple tree:

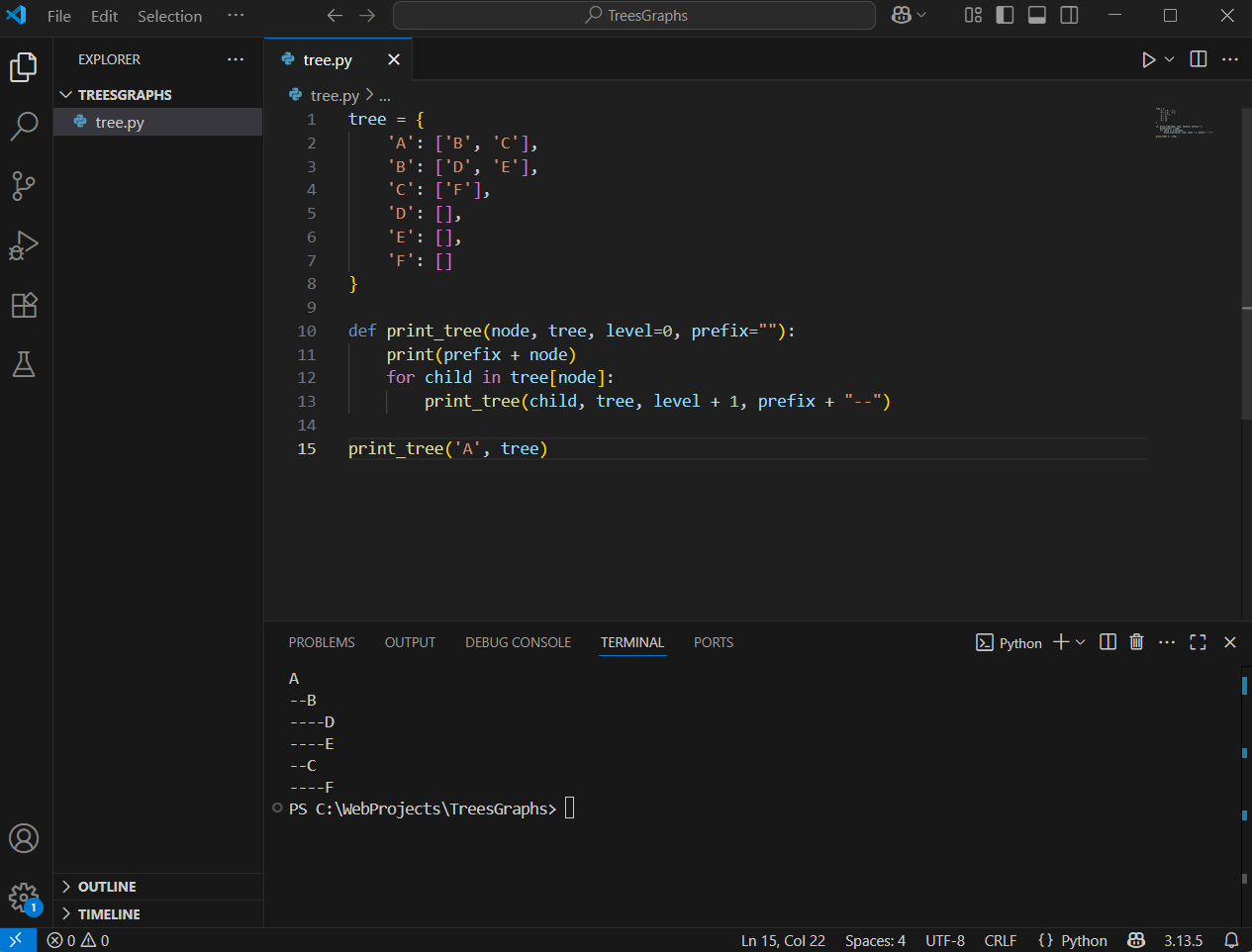
tree = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': [],
    'F': []
}

def print_tree(node, tree, level=0, prefix=""):
    print(prefix + node)
    for child in tree[node]:
        print_tree(child, tree, level + 1, prefix + "--")

print_tree('A', tree)

A graph is a collection of nodes (also called vertices) connected by edges. Unlike trees, which are strictly hierarchical and have no cycles, graphs are more flexible. They can have cycles, meaning you can start at a node, follow edges, and return to the starting node, and they don't have to follow a top-down structure. This makes graphs ideal for modelling complex networks, such as social media connections (where friends are linked), road maps, or even the internet with linked web pages.

Key terms:

• Vertex: A node in the graph, like a city in a map.
• Edge: A connection between vertices, which can be directed (one-way) or undirected (two-way).
• Cycle: A path that starts and ends at the same vertex, forming a loop.
• Directed Graph: Edges have a direction, like one-way streets or following someone on social media (A follows B, but not necessarily vice versa).
• Undirected Graph: Edges are bidirectional, like mutual friendships or two-way roads.

Graphs are incredibly versatile for representing real-world relationships and are used to solve problems like finding the shortest path between two points, detecting connections, or even recommending friends on social networks.

Next, we'll represent a graph in Python using a simple structure.

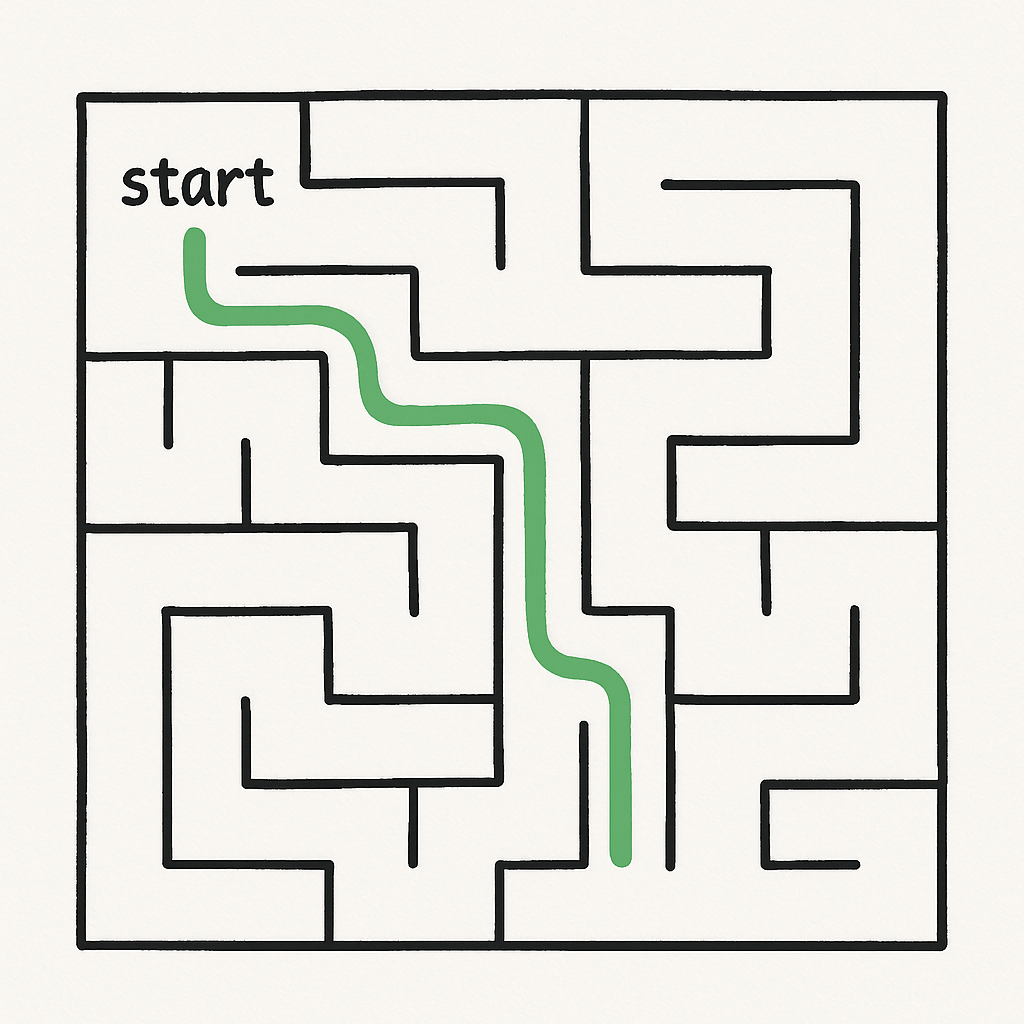DFS is a traversal algorithm that explores as far as possible along each branch before backtracking. It uses a stack (or recursion) and is useful for path-finding or detecting cycles.

In DFS, you start at a node, visit an unvisited neighbour, and repeat recursively. If no unvisited neighbours, backtrack.

Imagine you're exploring a maze: you pick one path and follow it as deep as you can until you hit a dead end, then you backtrack to the last junction and try a different path. This 'depth-first' approach means you explore one branch thoroughly before moving to the next, which is great for finding any path quickly, even if it's not the shortest one.

Next, you'll implement DFS on the graph.