In this lesson on logic gates and Boolean algebra, you'll explore fundamental concepts in computer science that help you understand how computers make decisions and process information at the hardware level. We'll cover the following main topics:

1. What logic gates are, including the basic types: AND, OR, and NOT, with everyday examples.
2. Circuit diagrams and truth tables for these gates.
3. The basics of Boolean algebra, including variables, operators, and key laws for simplifying expressions.
4. Practical tasks using MakeCode for the micro:bit to simulate logic gates and apply Boolean concepts.

Let's start with the basics. Computers as super-smart machines that make decisions all the time, but at their core, they use something very simple: yes or no answers. This is where logic gates come in. Logic gates are like tiny decision-makers inside a computer's hardware. They take in simple inputs – which are just binary numbers, meaning 0 (for 'false' or 'off') or 1 (for 'true' or 'on') – and based on those, they produce an output that's also a 0 or 1.

Think of binary like a light switch: off (0) or on (1). Logic gates process these switches to help the computer do everything from playing games to browsing the internet. There are three basic types of logic gates we'll focus on: AND, OR, and NOT. We'll explain each one with everyday examples to make it easier to understand.

• AND Gate: This gate only says 'yes' (outputs 1) if both inputs are 'yes' (1). If even one is 'no' (0), the output is 'no' (0). Real-life example: You can complete an online transaction only if you enter the correct credit card number AND the correct CVV code. It's like saying 'both this AND that must be true'.
• OR Gate: This one says 'yes' (outputs 1) if at least one input is 'yes' (1). It only says 'no' (0) if both inputs are 'no' (0). Example: You can enter a building if you have a key OR know the code. As long as one is true, you're in. It's like 'this OR that is true'.
• NOT Gate: This is a simple inverter – it flips the input. If the input is 1, output is 0; if input is 0, output is 1. Example: If it's not raining (NOT raining), you don't need an umbrella. It just reverses whatever you give it, like saying 'NOT this'.

These gates might seem basic, but when you combine lots of them, they create the complex circuits that power computers. For instance, they're used in the CPU (the brain of the computer) to do things like adding numbers or making choices in programs. 

Let's understand what circuit diagrams and truth tables are.

Circuit diagrams are like maps that show how electronic components, such as logic gates, are connected together to form a complete circuit. They use standard symbols to represent each type of gate, making it easier to visualise and design digital systems without needing the actual hardware.

Truth tables, on the other hand, are simple tables that list every possible combination of input values (0s and 1s) for a logic gate or circuit, along with the corresponding output. They help us verify how a gate behaves and are essential for understanding and designing logic circuits.

Now, let's look at the truth tables and circuit diagrams for the basic gates.

AND Gate

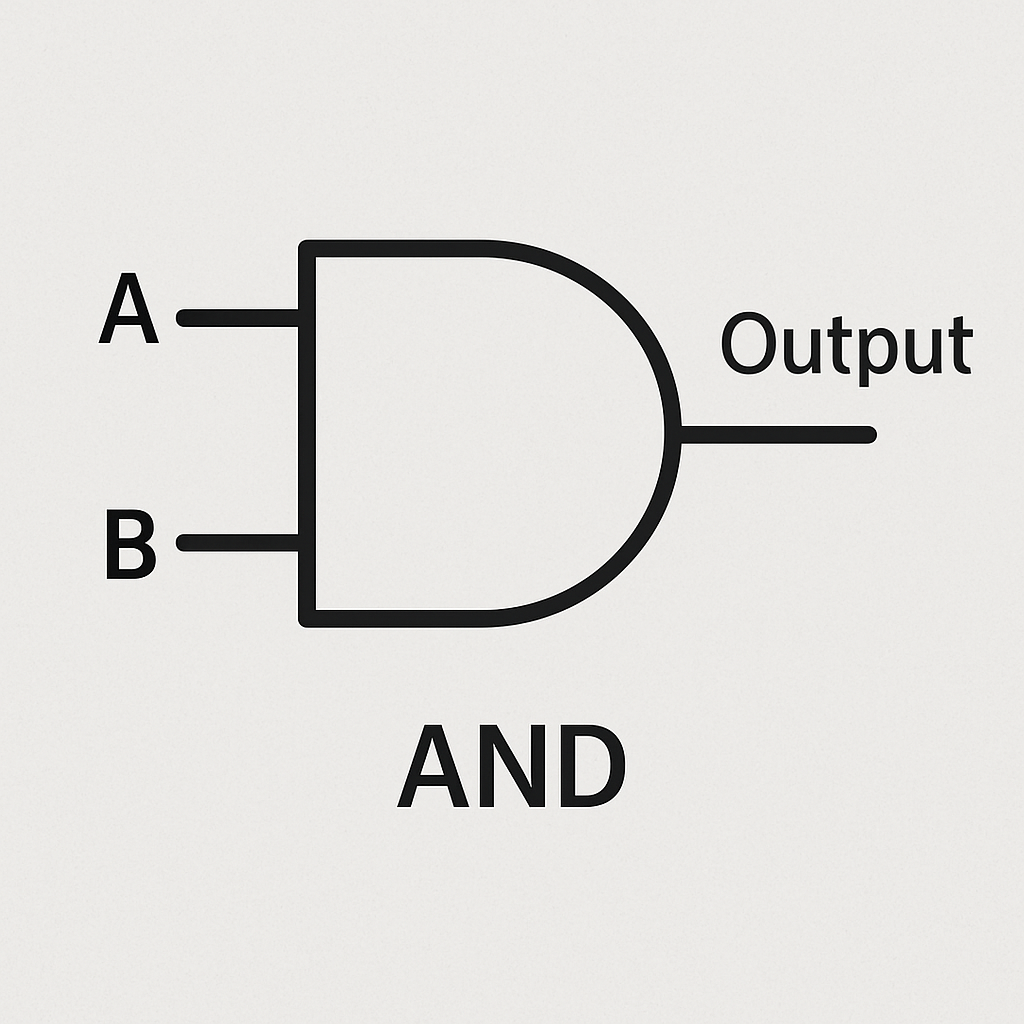
A	B	Output (A AND B)
0	0	0
0	1	0
1	0	0
1	1	1

OR Gate

A	B	Output (A OR B)
0	0	0
0	1	1
1	0	1
1	1	1

NOT Gate

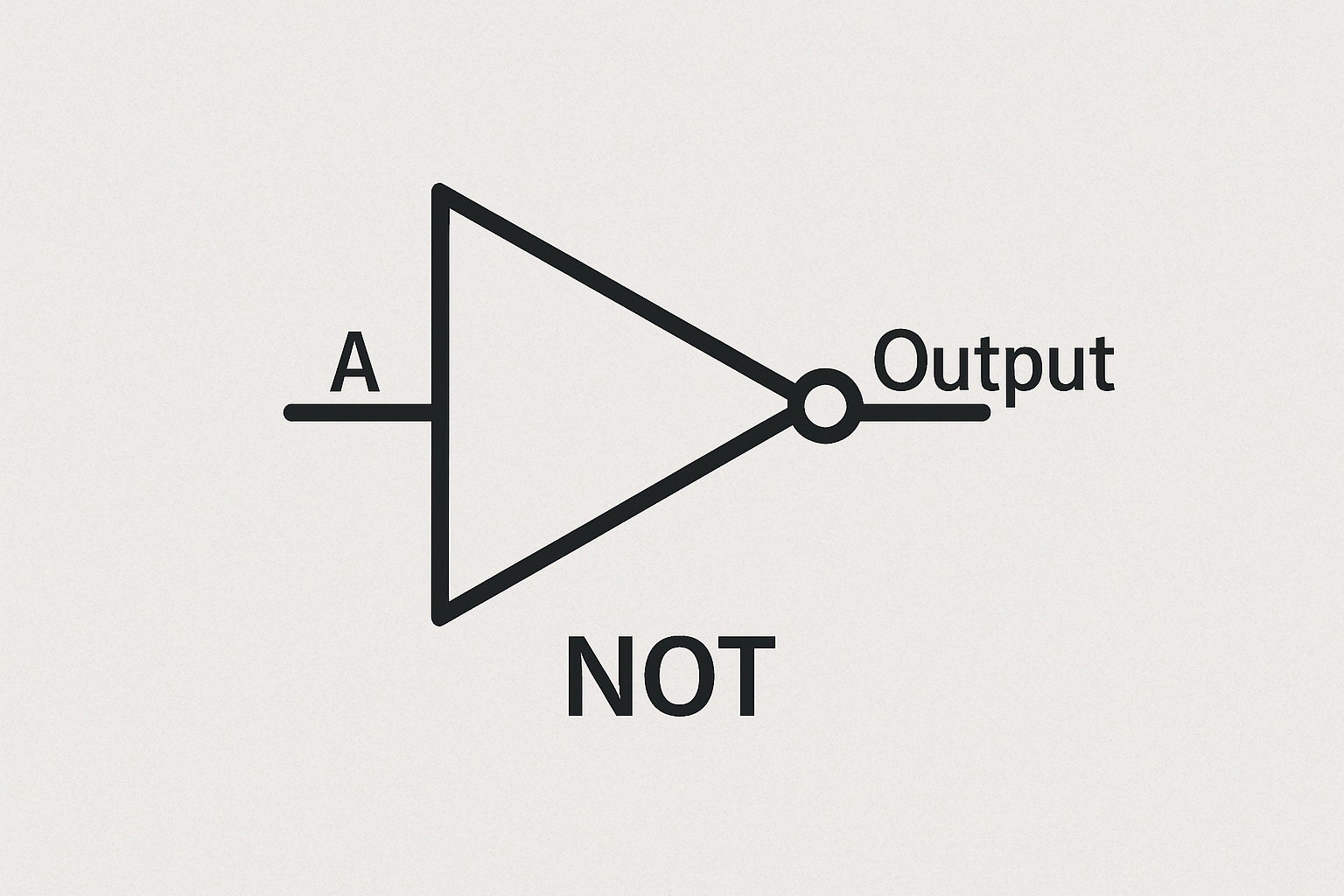
A	Output (NOT A)
0	1
1	0

Now lets create a simple program that uses if-then statements with AND and OR logical operators. These operators work just like the AND and OR gates in the previous step.

Open the MakeCode editor at makecode.microbit.org and start a new project.

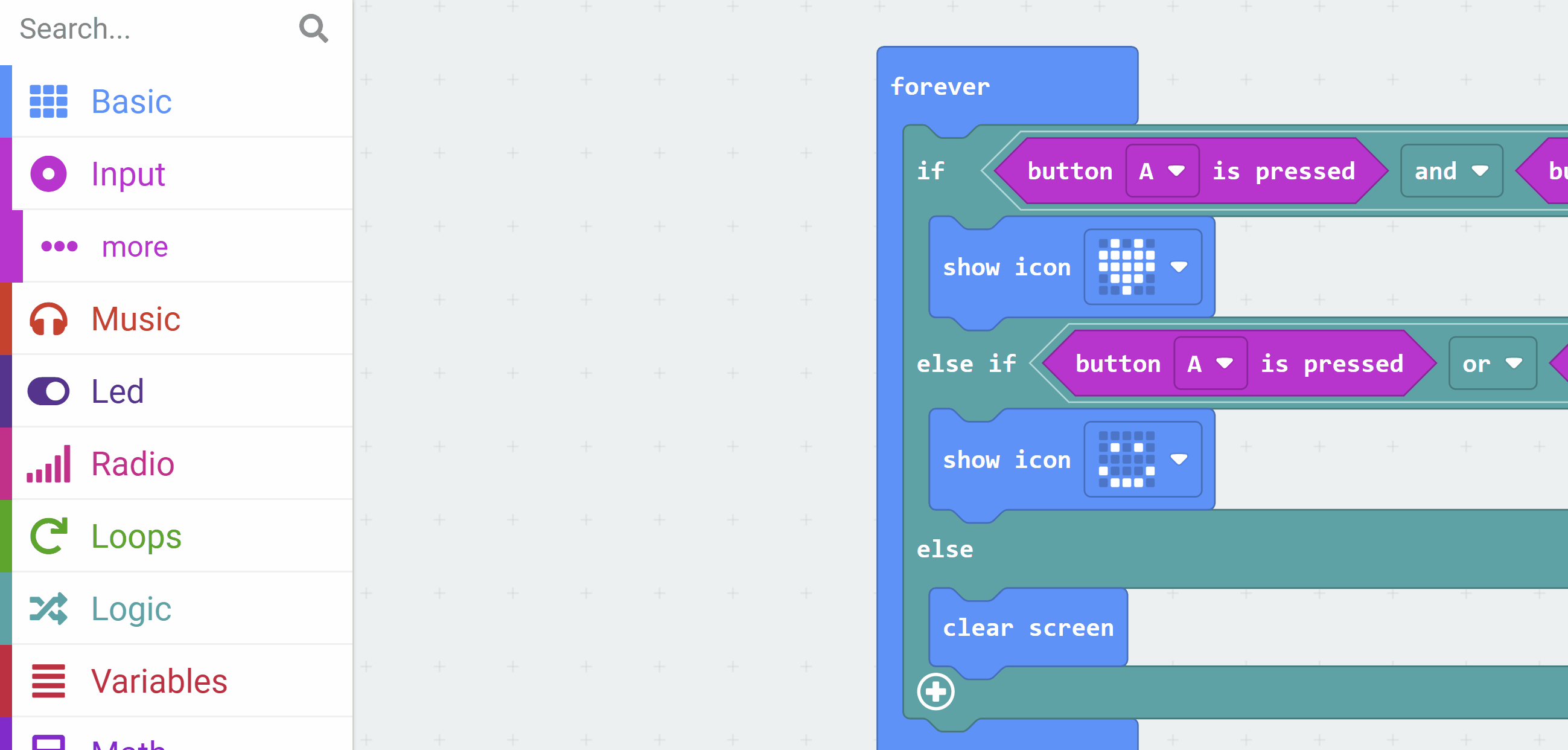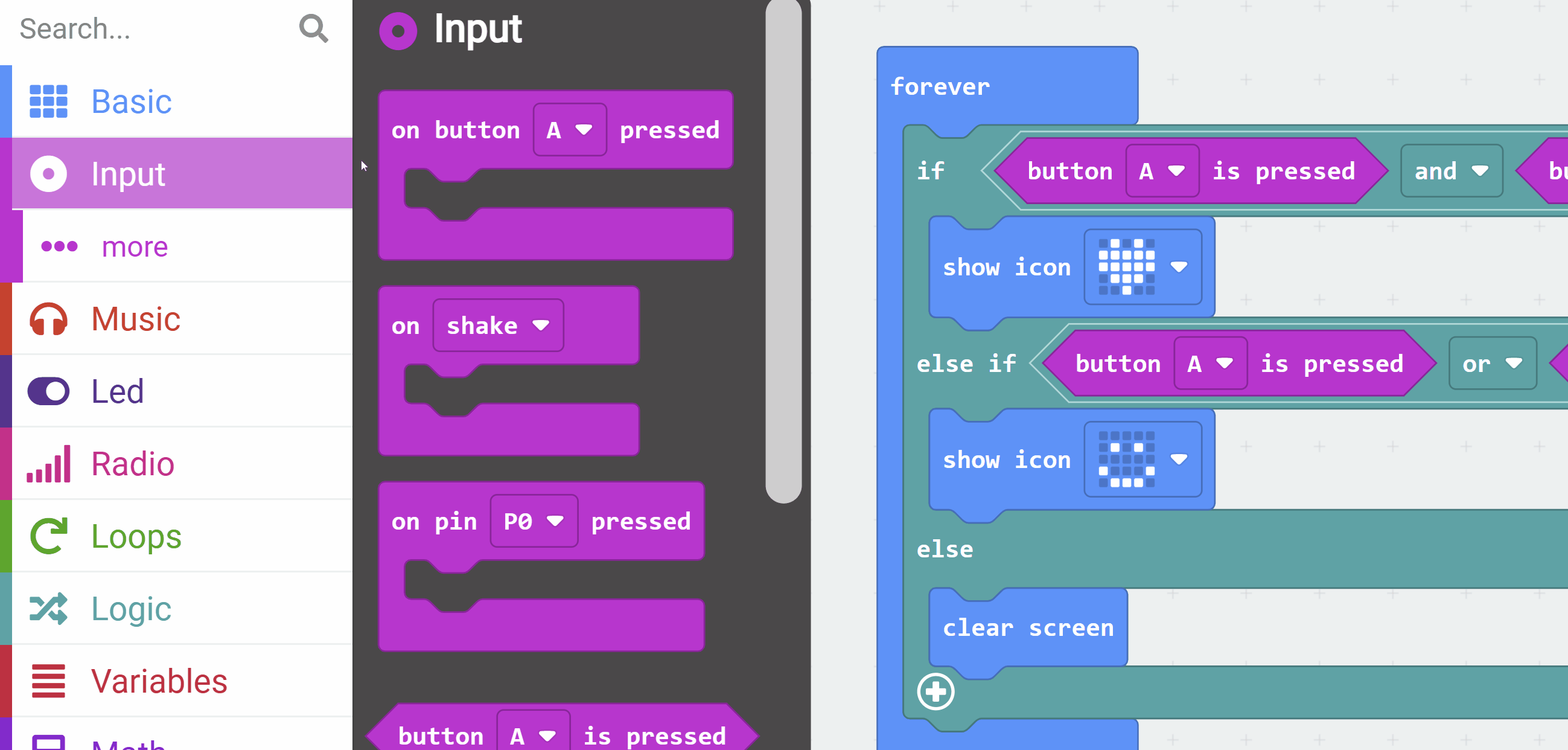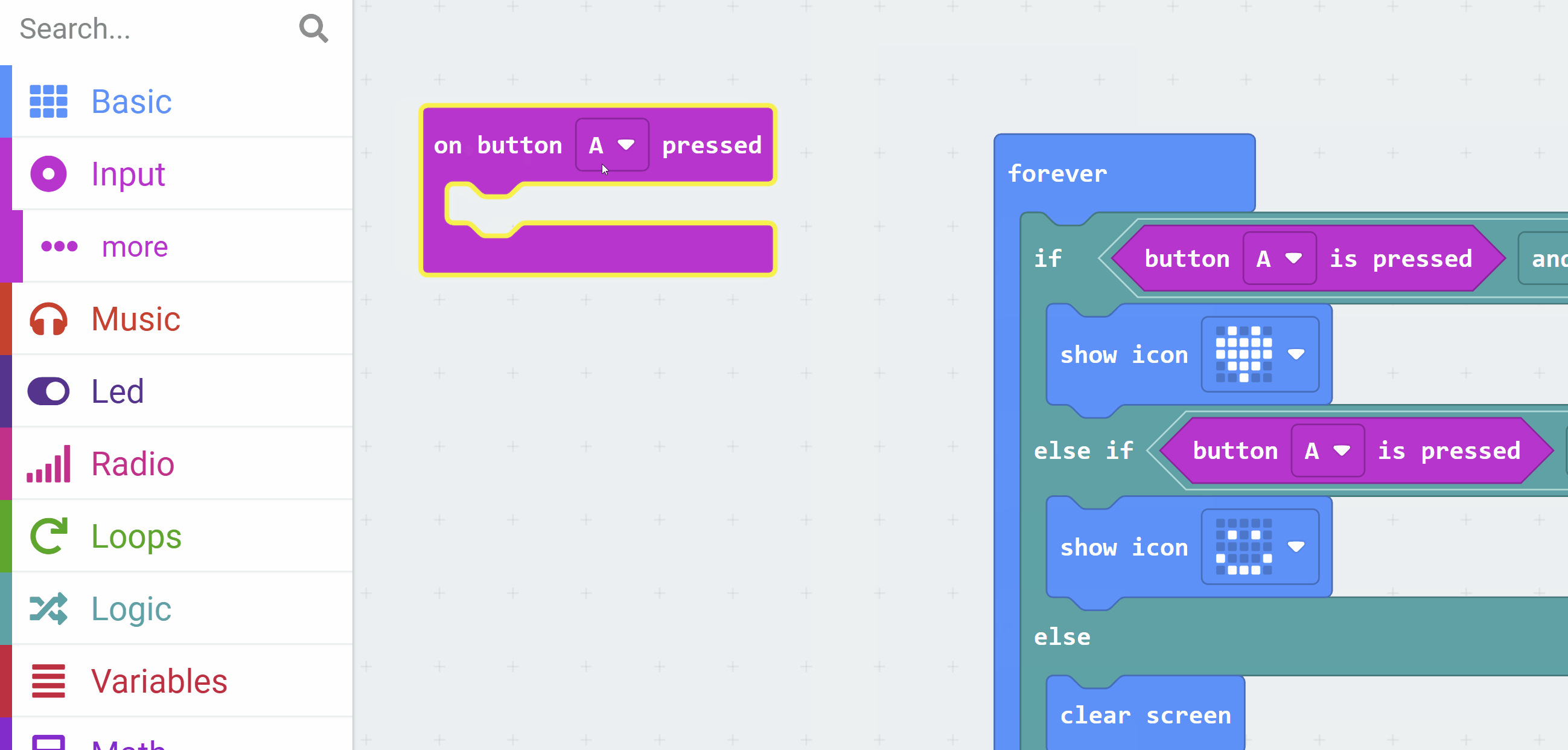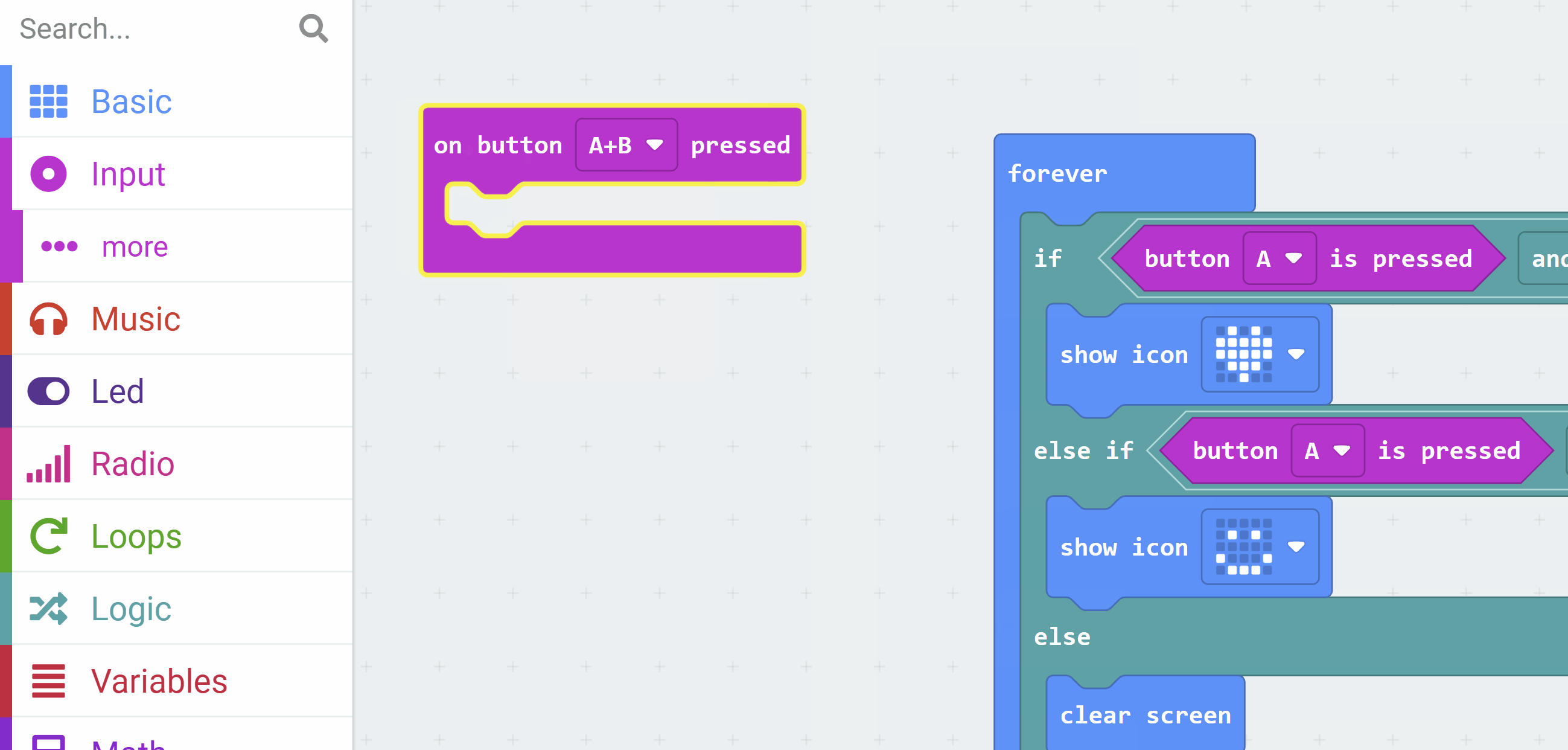
The goal is to create a program that checks button presses continuously and displays different icons based on logic conditions:

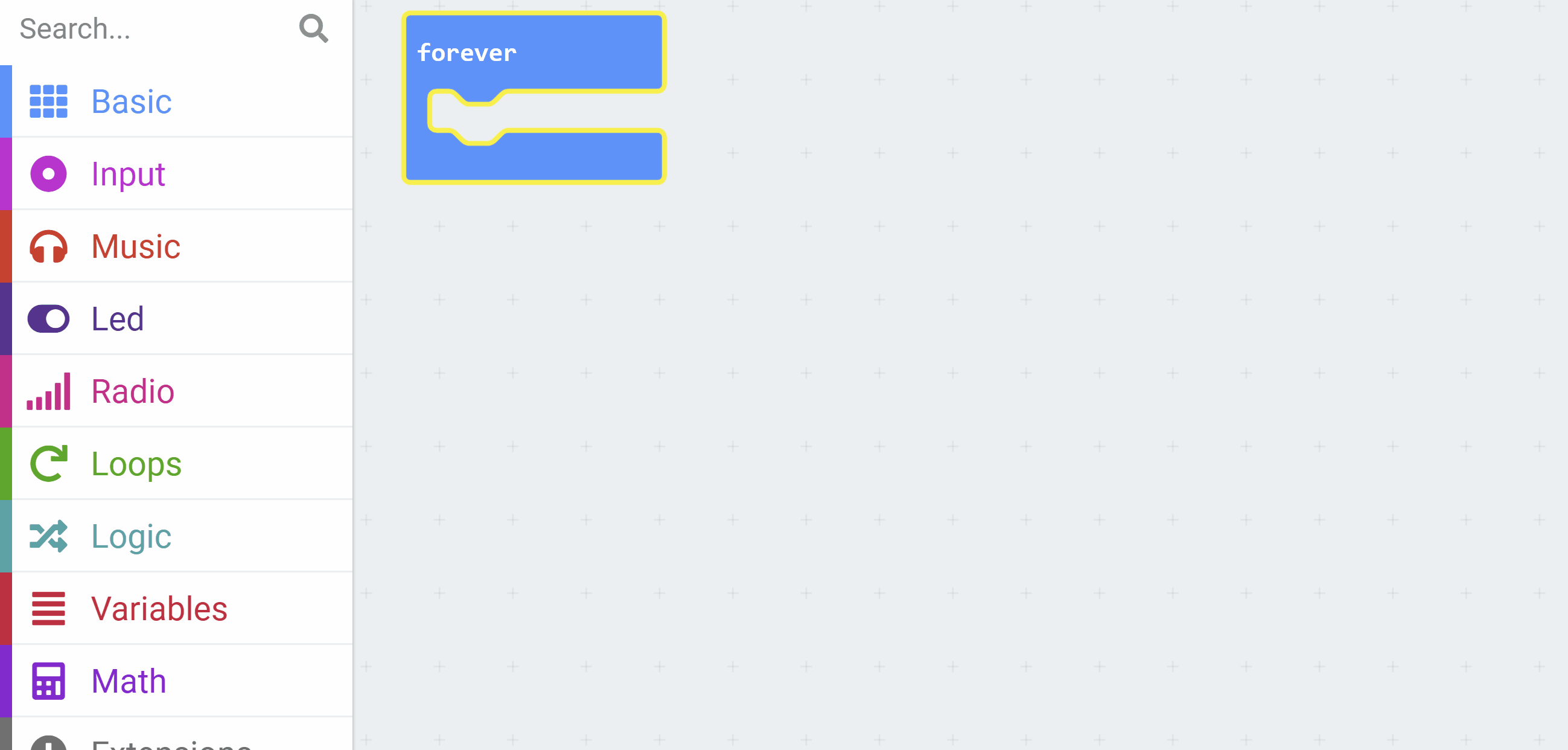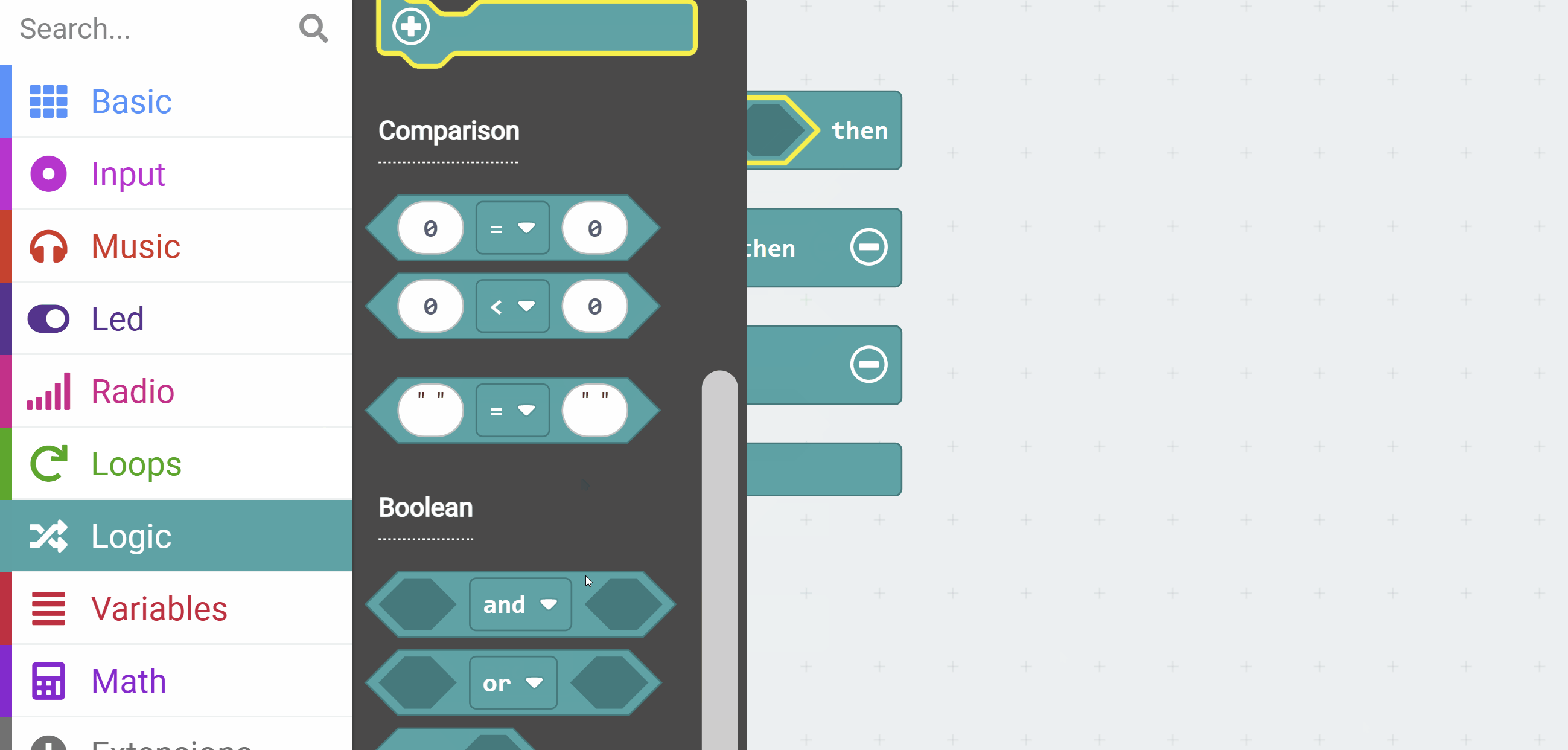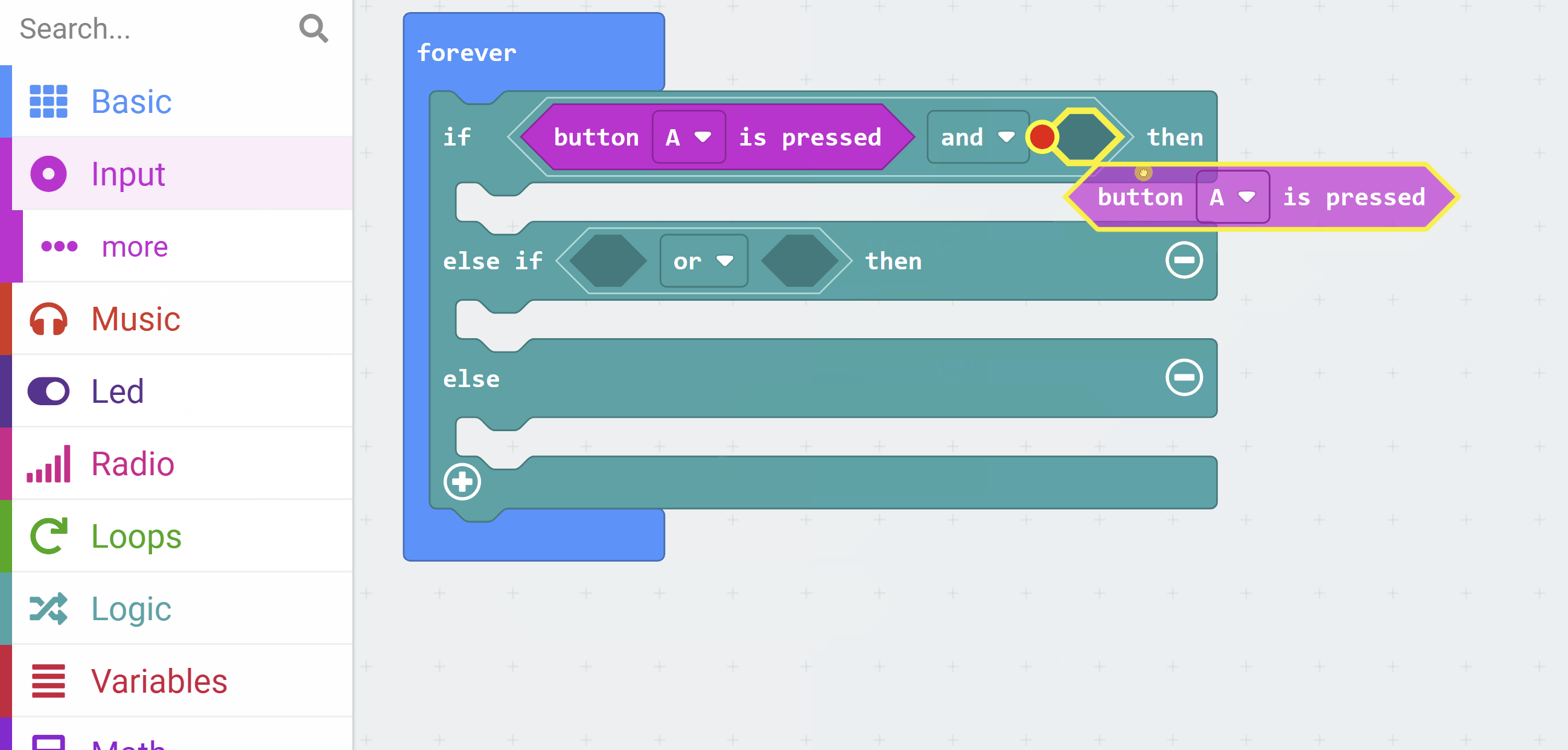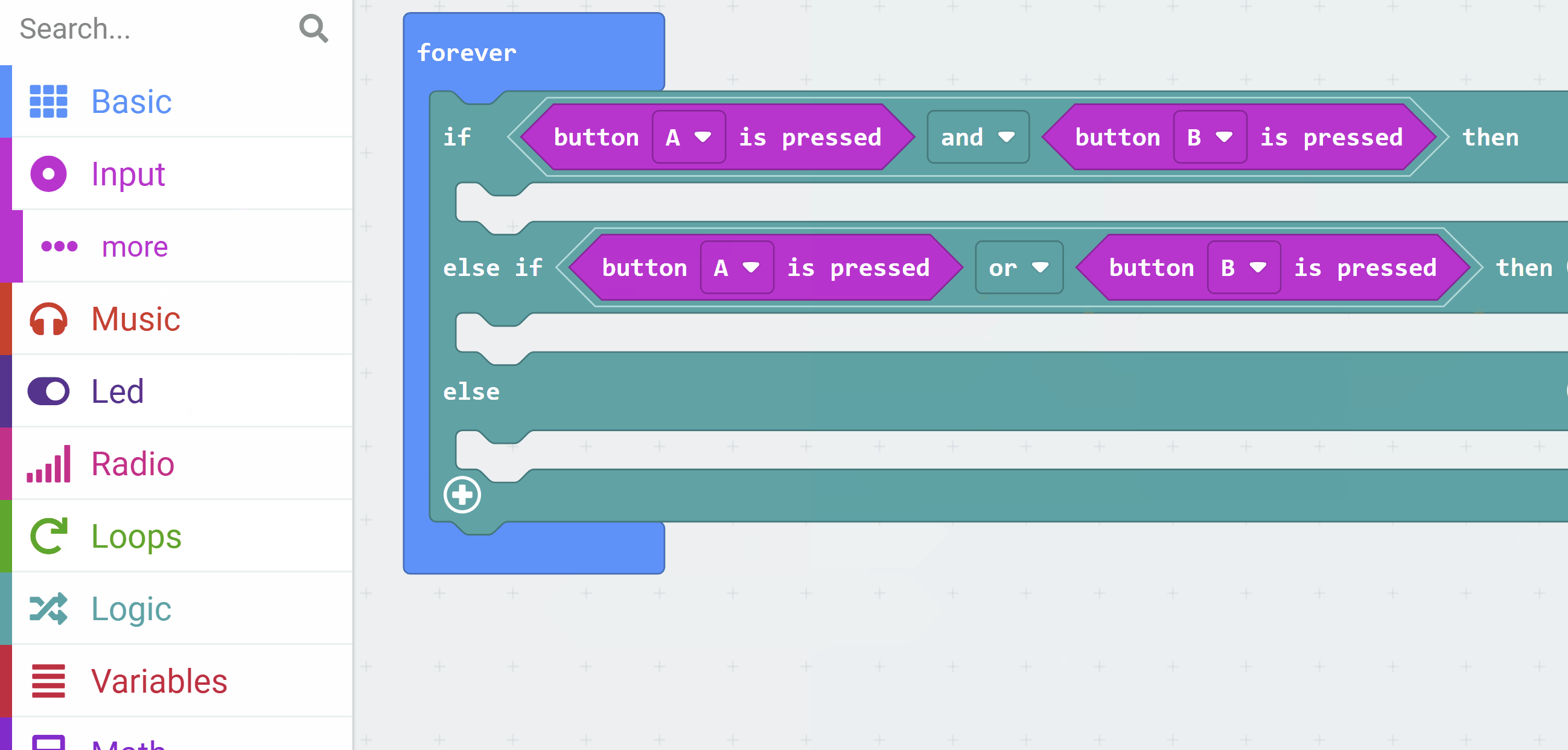
• If both button A AND button B are pressed, show a heart icon (simulating an AND gate).
• Else if button A OR button B is pressed, show a happy face icon (simulating an OR gate).
• Otherwise, clear the screen.

This will run in a loop to constantly check the buttons.

This code simulates the gates by prioritising the AND condition first, so when both buttons are pressed, it shows the heart instead of the happy face.

Add the following code:

input.onButtonPressed(Button.AB, function () {	})basic.forever(function () {    if (input.buttonIsPressed(Button.A) && input.buttonIsPressed(Button.B)) {        basic.showIcon(IconNames.Heart)    } else if (input.buttonIsPressed(Button.A) || input.buttonIsPressed(Button.B)) {        basic.showIcon(IconNames.Happy)    } else {        basic.clearScreen()    }})

Now that you've learned about logic gates and how they work with binary inputs, let's dive into Boolean algebra. Don't worry if it sounds a bit mathematical – it's actually a simple way to describe and work with the logic we've been talking about. Boolean algebra is named after George Boole, a mathematician who came up with it in the 1800s, and it's the foundation of how computers handle decisions.

At its core, Boolean algebra is a system of maths that deals with true and false values – remember, that's 1 for true and 0 for false, just like in logic gates. It allows us to write down logic expressions using variables and special operators, and then simplify them. This is super useful because it helps engineers design smaller, faster, and cheaper computer circuits by reducing the number of gates needed.

Let's break it down step by step.

Variables in Boolean Algebra

Variables are just placeholders for binary values. We usually use letters like A, B, or C. Each can be either 0 (false) or 1 (true). For example, A might represent whether button A is pressed (1) or not (0).

Operators in Boolean Algebra

There are three main operators that match the logic gates we've seen:

• AND: Written as A · B (with a dot) or sometimes just AB (no symbol). It means both A and B must be 1 for the result to be 1. Example: If A is 'it's raining' (1 if true) and B is 'I have an umbrella' (1 if true), then A · B means 'it's raining AND I have an umbrella' – only true if both are 1.
• OR: Written as A + B. It means the result is 1 if at least one of A or B is 1. Example: A + B could be 'I can pay with cash OR card' – true if you have either (or both).
• NOT: Written as Ā (with a bar over A) or sometimes A'. It flips the value: if A is 1, Ā is 0, and vice versa. Example: If A is 'light is on' (1), then Ā is 'light is off' (0).

You can combine these to make more complex expressions, like (A · B) + Ā, which means '(A AND B) OR NOT A'.

Basic Laws of Boolean Algebra

Just like regular algebra has rules, Boolean algebra has laws that help us simplify expressions. Here are a few key ones explained simply:

• Commutative Law: The order doesn't matter. For OR: A + B = B + A. For AND: A · B = B · A. Example: 'Apple OR Banana' is the same as 'Banana OR Apple'.
• Associative Law: Grouping doesn't matter when you have three or more. For OR: (A + B) + C = A + (B + C). For AND: (A · B) · C = A · (B · C). This lets you rearrange parentheses without changing the meaning.
• Identity Law: Adding 0 or multiplying by 1 doesn't change the value. For OR: A + 0 = A (like saying 'A OR false' is just A). For AND: A · 1 = A ( 'A AND true' is just A).

There are more laws, like distributive and De Morgan's, but we'll stick to these basics for now. The good part is using these laws to simplify expressions. For example, if you have A · (A + B), using distributive law, it becomes A · A + A · B, and since A · A is just A, it simplifies to A + A · B.

Why does this matter? In real life, simplifying a Boolean expression means you can build a circuit with fewer gates, which saves space and power in devices like your phone or computer.

Take a moment to think about how this connects back to the logic gates. Each operator directly represents a gate: · for AND gate, + for OR gate, ¯ for NOT gate.