In this lesson, you'll explore the fundamentals of algorithms, which form the backbone of computer science and programming. You'll learn how algorithms work as step-by-step instructions to solve problems, and you'll get hands-on experience visualising them through flowcharts. This will help you think logically and plan solutions effectively, skills that are crucial for coding and beyond.

You'll cover the following main areas:

1. What an algorithm is and its importance in computing.
2. Key properties that make algorithms effective and reliable.
3. An introduction to flowcharts and how they help visualise algorithms.
4. A practical task to draw a flowchart using pen and paper.
5. A practical task to recreate your flowchart using an online tool.

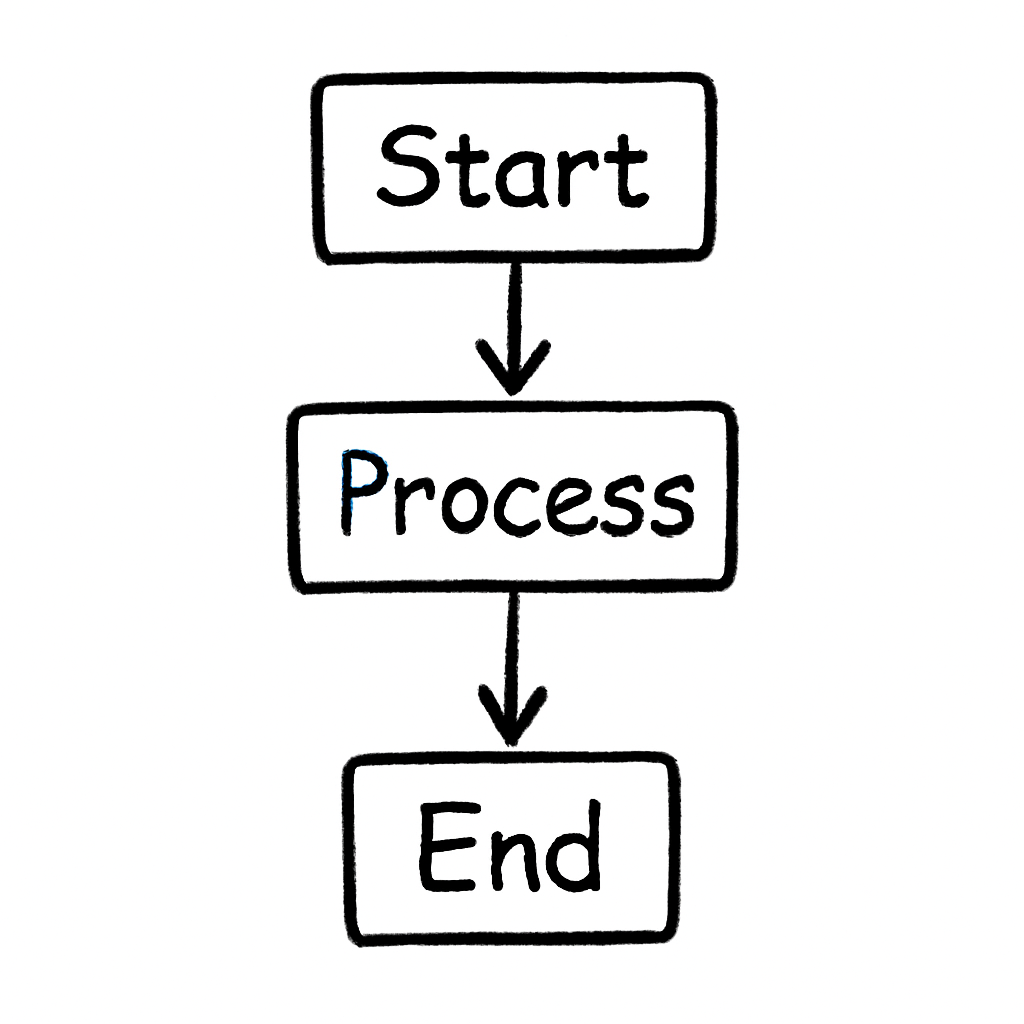An algorithm is simply a step-by-step set of instructions that helps you solve a problem or complete a task. Imagine it as a clear guide that tells you exactly what to do, one thing at a time, in the right order, so you end up with the result you want.

Think of it like following a recipe to make your favourite sandwich. The recipe might say:

1. Get two slices of bread.
2. Spread butter on one slice.
3. Add cheese and ham.
4. Put the other slice on top.
5. Cut it in half. 

If you follow these steps exactly, you get a perfect sandwich every time! That's an algorithm—it's all about breaking things down into simple, ordered steps.

Now, why is this important in computers? Computers can't think like we do; they need these precise instructions to do anything. Algorithms are the building blocks of computer science. They help computers process information, make choices, and solve problems. For example, when you search for something online, an algorithm quickly finds the best results for you. Or on social media, algorithms decide what posts show up in your feed based on what you like.

Good algorithms share certain properties that make them effective and reliable. Understanding these properties will help you design better algorithms in your coding projects. Let's explore each one in detail, with examples to make them clearer.

Precision

An algorithm must be precise, meaning every step is clear, specific, and leaves no room for confusion or different interpretations. Think of it like giving directions to a friend: if you say "turn left at the big tree," it might be ambiguous if there are multiple trees. A precise algorithm would say "turn left at the oak tree next to the green postbox."

Finiteness

Algorithms must be finite, which means they have a clear beginning and end, and they don't go on forever. They should complete in a reasonable number of steps.

Effectiveness

An algorithm needs to be effective, solving the problem correctly and producing the right output for any valid input.

Efficiency

Finally, good algorithms are efficient, using resources like time and memory wisely. They should solve the problem as quickly as possible without wasting unnecessary steps.

Remember, not all algorithms need to be perfectly efficient for simple tasks, but in computing, efficiency becomes crucial for handling large amounts of data. As you create your own algorithms, try to check if they meet these properties.

Flowcharts are a fantastic way to visualise algorithms. They use simple shapes and arrows to represent the steps in a process, making it easier to plan, understand, and debug your ideas before you start coding. Think of a flowchart as a map that guides you through the logic of an algorithm, showing how decisions lead to different paths.

Why Use Flowcharts?

Flowcharts help break down complex problems into manageable steps. They are especially useful in programming because they allow you to spot errors or inefficiencies early on. For example, if you're designing a game or an app, a flowchart can outline the user choices and outcomes without writing a single line of code.

Basic Shapes in Flowcharts

Flowcharts use standard shapes to represent different types of actions. Here's a quick guide to the most common ones:

Oval

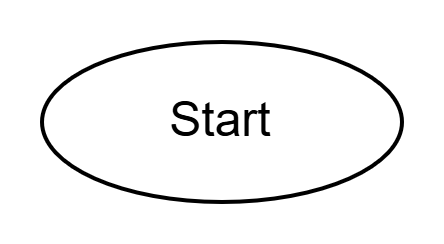
Used for the start and end of the algorithm. It marks where the process begins and finishes.

Rectangle

Represents a process or action step, like "Display a message" or "Calculate a sum".

Diamond

Indicates a decision point, where the flow branches based on a yes/no question, such as "Is it raining?".

Parallelogram

Often used for input or output, like reading data from a user or showing results.

Arrow

Shows the direction of the flow, connecting the shapes in the correct order.

A Simple Example: Checking the Weather

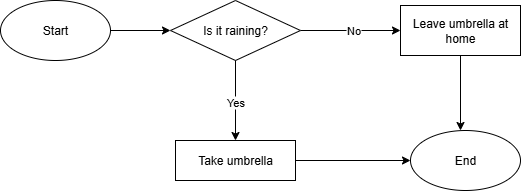
Let's create a flowchart for a basic algorithm that decides whether to take an umbrella based on the weather.

1. Start (oval).
2. Is it raining? (diamond).
3. If yes, arrow to "Take umbrella" (rectangle), then to End (oval).
4. If no, arrow to "Leave umbrella at home" (rectangle), then to End (oval).

Now it's your turn to practice what you've learned about flowcharts. For this task, you'll create your own flowchart using just a pen and paper. This will help you understand how to break down a simple everyday task into an algorithm and visualise it with the shapes we've discussed.

Choose a simple task from your daily life, such as 'making a sandwich' (like the example in the first step), 'getting ready for school', or 'checking if you need an umbrella'. If you're stuck, use the sandwich example.