 In this lesson you'll learn about time and space complexity, Big O notation, and apply these concepts by implementing and timing sorting algorithms in Python using VS Code.
In this lesson you'll learn about time and space complexity, Big O notation, and apply these concepts by implementing and timing sorting algorithms in Python using VS Code.
By the end of this lesson, you will be able to:
You'll need VS Code installed with Python extension. Work in a new folder called 'AlgoEfficiency'.
 Algorithmic efficiency refers to how well an algorithm performs in terms of time (how fast it runs) and space (how much memory it uses). Efficient algorithms solve problems quickly and with minimal resources, which is crucial for large datasets, such as those in social media apps or scientific simulations where speed and low resource use can make a big difference.
Algorithmic efficiency refers to how well an algorithm performs in terms of time (how fast it runs) and space (how much memory it uses). Efficient algorithms solve problems quickly and with minimal resources, which is crucial for large datasets, such as those in social media apps or scientific simulations where speed and low resource use can make a big difference.
Time complexity measures the time an algorithm takes as the input size grows. Space complexity measures the memory used.
In the next steps, we'll explore these concepts in detail.
 Time complexity helps us understand how the running time of an algorithm increases as the size of the input (often denoted as 'n') gets larger. It's a way to predict how efficient an algorithm will be for big problems, without worrying about the exact hardware or small details.
Time complexity helps us understand how the running time of an algorithm increases as the size of the input (often denoted as 'n') gets larger. It's a way to predict how efficient an algorithm will be for big problems, without worrying about the exact hardware or small details.
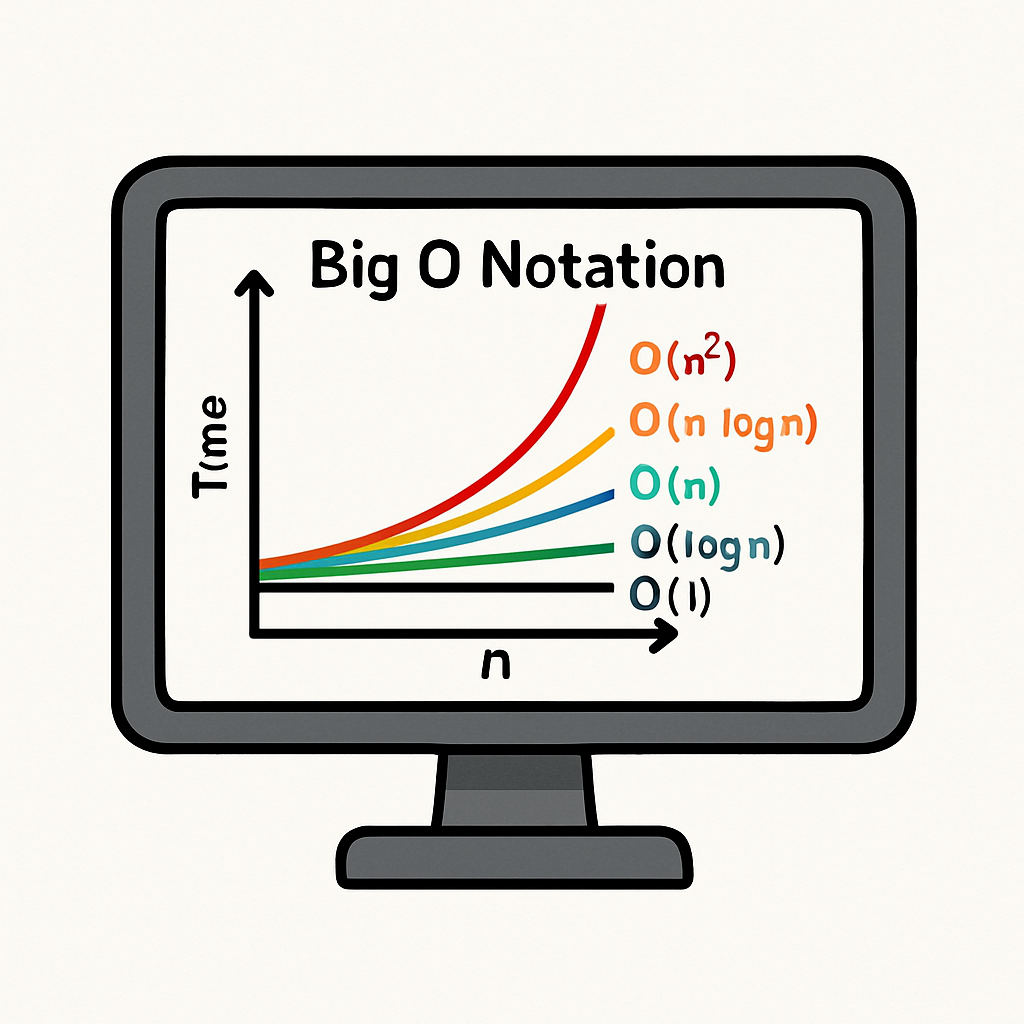
This is expressed using Big O notation, which focuses on the worst-case scenario – the maximum time an algorithm might take for a given input size. Big O gives us an upper bound on the growth rate, ignoring constant factors and smaller terms to focus on the big picture.
Here are some common Big O notations, explained with examples:



In sorting algorithms, bubble sort has a time complexity of O(n²) because of its nested loops, making it inefficient for large datasets. Quicksort, on the other hand, has an average time complexity of O(n log n), which is much better – it grows slower than quadratic but faster than linear.
Understanding Big O helps you choose the right algorithm for the job, especially when dealing with large amounts of data.
 Space complexity measures how the memory usage of an algorithm increases as the size of the input (often denoted as 'n') gets larger. Just like time complexity, it's expressed using Big O notation, focusing on the worst-case scenario – the maximum memory an algorithm might require for a given input size.
Space complexity measures how the memory usage of an algorithm increases as the size of the input (often denoted as 'n') gets larger. Just like time complexity, it's expressed using Big O notation, focusing on the worst-case scenario – the maximum memory an algorithm might require for a given input size.
Space complexity considers both the space needed for the input itself and any additional (auxiliary) space used by the algorithm, such as temporary variables, recursion stacks, or extra data structures. Efficient space usage is important in environments with limited memory, like mobile devices or embedded systems, where using too much RAM can cause crashes or slow performance.
Here are some common Big O notations for space complexity, explained with examples:

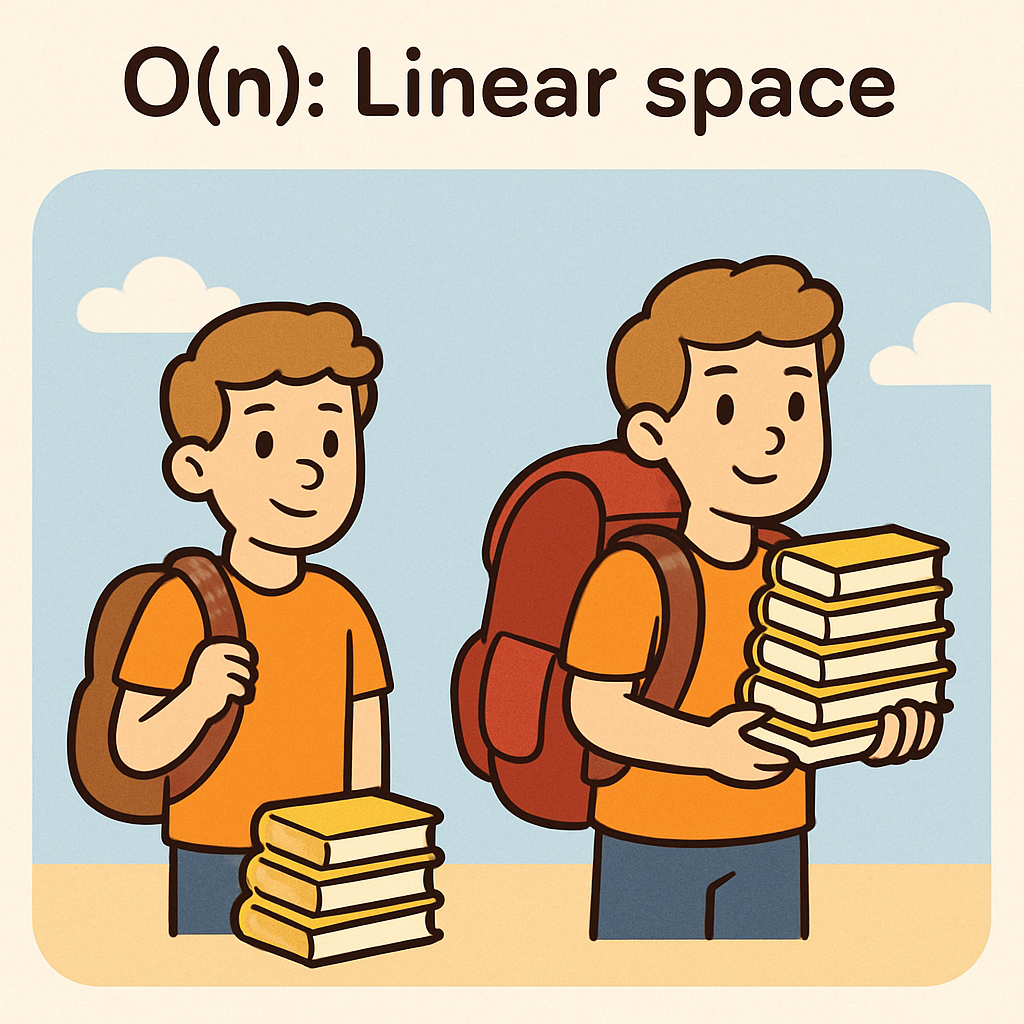
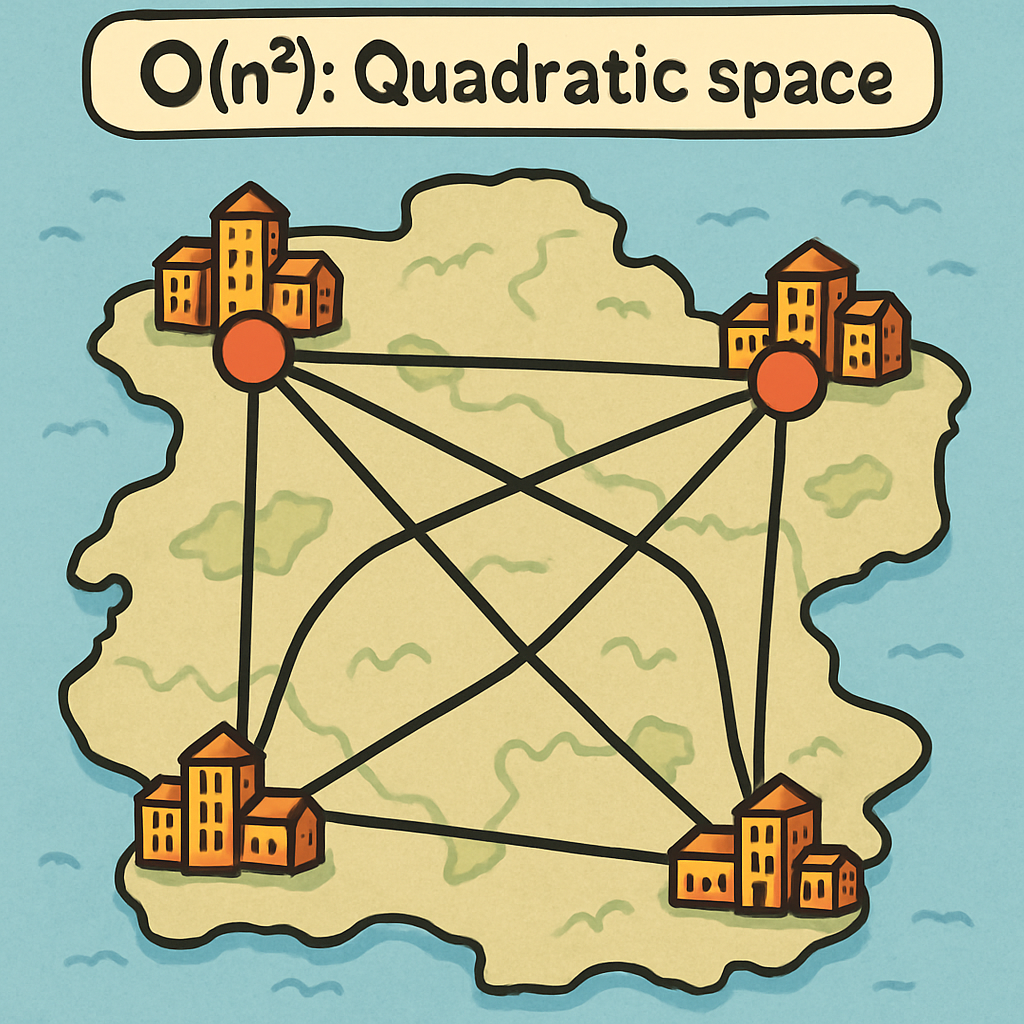
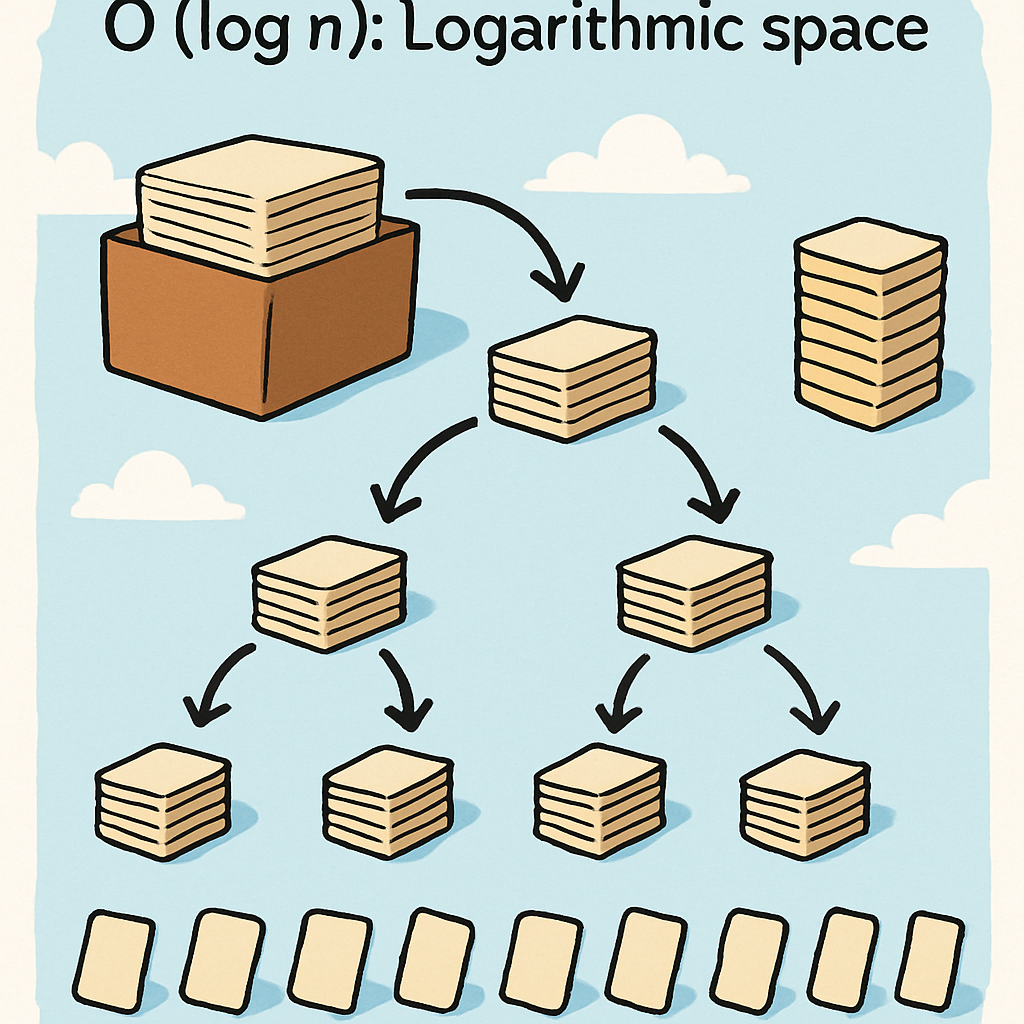
In sorting algorithms, bubble sort and insertion sort have O(1) space complexity because they sort in place, using only a few extra variables. Quicksort, however, has O(log n) space on average due to the recursion stack, though worst-case can be O(n).
Understanding space complexity helps you design algorithms that are not only fast but also memory-efficient, which is crucial for real-world applications.
Now, let's apply these concepts by implementing sorting algorithms and analysing their efficiencies.
Open VS Code and create a new folder called 'AlgoEfficiency'. Inside it, create a file named 'sorting.py'.
We'll implement three sorting algorithms: bubble sort (O(n²)), insertion sort (O(n²)), and quicksort (O(n log n) average).
We'll use Python's time module to measure execution time (to track how long each sorting algorithm takes) and random to generate test data (to create random lists of numbers for sorting).
Add this import code to 'sorting.py':
import time
import randomSave the file. We'll add functions next.